【教育】大学生でも間違える計算「40－16÷4÷2」

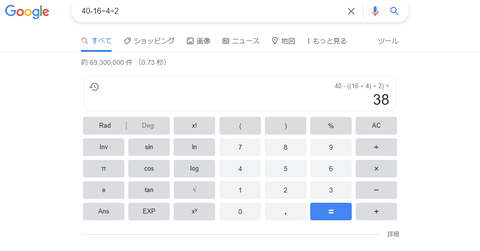
40-16÷4÷2　=　24÷4÷2　=　6÷2　=　3 ……(1)
40-16÷4÷2　=　24÷4÷2　=　24÷2　=　12 ……(2)
40-16÷4÷2　=　40-4÷2　=　36÷2　=　18 ……(3)
40-16÷4÷2　=　40-4÷2　=　40-2　=　38 ……(4)
40-16÷4÷2　=　40-16÷2　=　24÷2　=　12 ……(5)
40-16÷4÷2　=　40-16÷2　=　40-8　=　32 ……(6)

計算規則は以下の3つである。

(I)　原則として計算は左から順に行う。
(II)　カッコ( )は一まとめに見て、その中を先に計算する。
(III)　×÷は+-より結び付きが強く、+-より先に計算する。

他大学の教員にも手伝ってもらって、多くの大学生に本問のテストをした。
その結果、少なくても1割ぐらいの大学生は間違えることが分かった。なお誤答としては、(1)と(6)が多くあった。

【問2】
(1)打率0.333(1/3)の打者の第1打席も第2打席もアウトだった。それを見たA君は、「次の第3打席はそろそろヒットを打つ頃だよ」と話した。
(2)正常なコインを誰かが5回投げたところ、表が2回、裏が3回出た。その結果だけを聞いたA君は、「1回目に表が出た確率は、やはり 1/2 だよ」と話した。
———-

A君の発言は両方とも間違っている。

(1)について。次の第3打席もヒットを打つ確率は0.333(1/3)である。

(2)について。1回目に表が出た確率は 2/5 である。なぜならば、表が2回出る場合は次の10通りで(左側から1回目2回目、…、5回目と並ぶ)、そのうちの4通りが1回目に表が出ている。それら10通りは同様に確かであるから、求める確率は 4/10 である。

6/16(水) 7:02
https://news.yahoo.co.jp/articles/110807b924249d867e220115dac51d10b1905aa6